Intelligent systems development and formal analysis of air traffic controller-pilot interface with probabilistic timed automata by branching bi-simulation

Project leader: Shazada Muhammad Umair Khan, PhD, Associate Professor, Department of Intelligent Systems and Cybersecurity

Project Goal: This project aims to create an interface from Probabilistic Timed Automata (PTA) and perform formal verification through branching bisimulation analysis. The main objective is to establish predictable and safe operator-automated system interaction under both probabilistic uncertainty and strict real-time constraints.

1. The research verifies system properties by behavioral equivalence analysis to confirm that the target system behaves identically to a reference system while protecting against external observation or intrusion.
2. The research identifies basic activities of user interface design to create systematic and effective development methods.
3. The research evaluates multiple user interaction approaches by studying their distinctive features and practical uses and their impact on usability.
4. The research develops design principles to improve supervisory control interfaces and user interface reliability through the elimination of error-prone states.
5. The research will be published.

This work establishes objectives to improve software system reliability and usability and security with emphasis on user interface and system behavior. The first objective involves formal property verification through behavioral equivalence to protect systems from external observation while maintaining confidentiality. The second and third objectives focus on user interface design and interaction aspects by identifying essential design activities and assessing multiple interaction styles to enhance user experience. The last objective aims to develop strong design principles which enable supervisory control and prevent system errors and failures in user interfaces. These goals work together to create software systems that are secure and user-focused and resistant to faults.

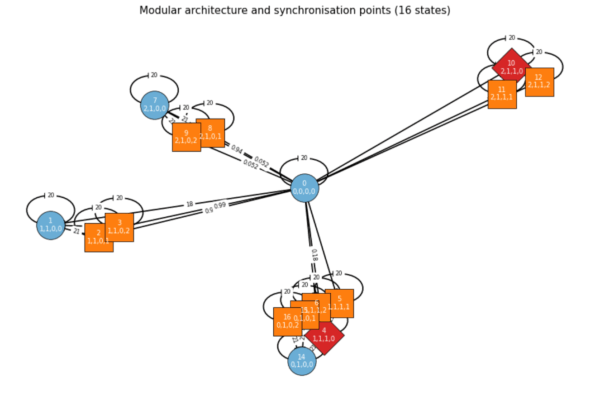
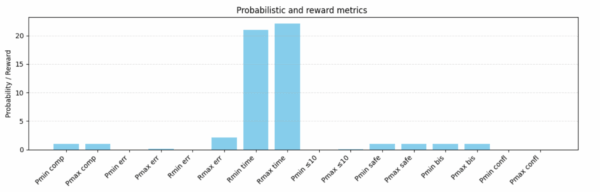
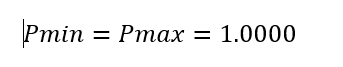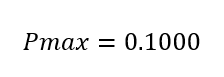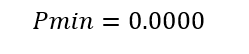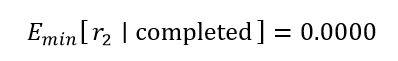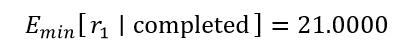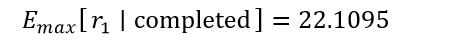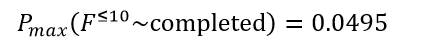1. All controller–pilot, avionics, and supervisory interactions from the requirements capture procedure led to a 358-state Markov decision process (MDP) that precisely models the probabilistic timed automaton. The global timer t used twenty-tick cycles to represent real-time deadlines through a one-and-a-half-second tick duration (see Figure 1).

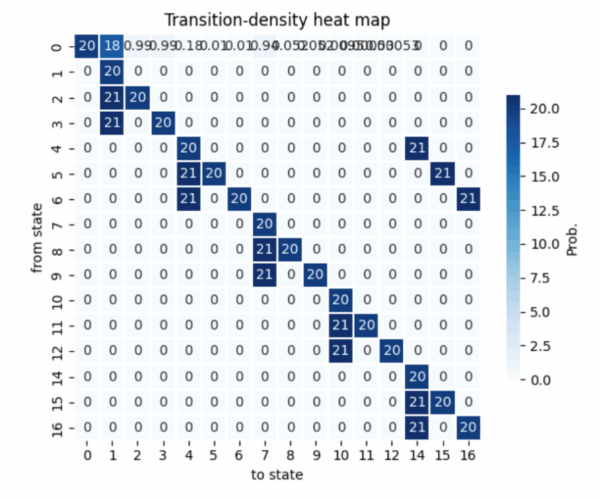
2. The composed MDP underwent breadth-first exploration which achieved convergence at 23 iterations to reveal 946 probabilistic transitions. The Bellman equations received value-iteration solutions for reachability and reward expectations which achieved a residual below  to confirm numerical soundness for both pessimistic and optimistic scheduler resolutions.

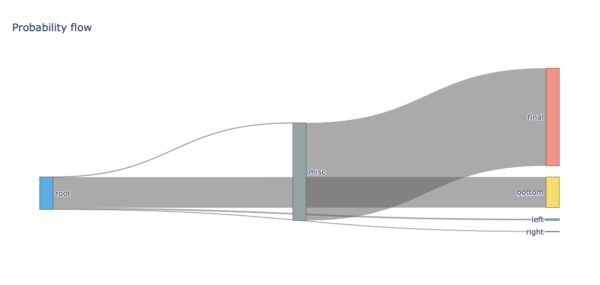
3. A total of sixteen PTCTL properties underwent evaluation. Any adversarial or cooperative scheduling policy leads to inevitable mission termination because unconditional reachability of the terminal label (“completed”) proved both 

worst-case slip probability  showed that error likelihood reached its maximum at ten percent of all executions

the best-case slip probability indicated that particular scheduler strategies could prevent crew-induced deviations completely.

4. The Reward Structure  evaluated the expected number of slips until the mission ended.

The most beneficial scheduling produced 

the most detrimental scheduling produced

thus revealing how scheduling decisions impact reliability.

5. The Reward Structure  measured completion time by tracking the number of ticks.

The smallest expected value of r_1 given completion was

while the highest value was

indicating a restricted time frame.

6. The ten-tick service objective led to bounded-time reachability where 

that only 4.95 % of traces satisfied the deadline while showing the delay from internal confirmation loops.

7. The safety invariant:

maintained its validity at probability one for all scheduling options which ensured no crew slips occurred after mission completion.

The bisimulation invariant

showed that the observable interface stayed semantically aligned with the concealed avionics model throughout the entire execution

8.  The supervisory veto mechanism operated with complete coherence because 

all possible adversarial scheduling choices.

9. The graph-theoretic decomposition process using Kosaraju’s algorithm revealed three strongly connected components that consisted of waiting, confirmation and dispatch. The confirmation SCC maintained a stationary probability mass distribution of approximately 70 % as indicated by its dominant diagonal band in the transition-density heat map (Figure 2) and its broad ribbon in the Sankey diagram of probability flow (Figure 3).

10. All probabilistic and reward metrics receive graphical comparison in the bar chart of Figure 4 to show the tight probability bounds for completion versus the extensive error count and latency variations.

The complete quantitative envelope is summarized in Table 1 which is presented next to Figure 2.

Table 1. Baseline PTZ model receives its quantitative results as described below

Figure 1. The modular system structure together with synchronization points (16 states) forms the basis of the system. The system contains nine PRISM modules that communicate through four broadcast actions: input, feedback, u_done and force_done as well as the global timer t. The Fruchterman–Reingold positioning technique arranges state-transition probabilities on each edge of the visual layout.

Figure 2. Transition-density heat map. The matrix organizes the three operational SCCs—waiting, confirmation, dispatch—into sequential blocks which run along the diagonal. Pixel intensity indicates transition probability; the confirmation SCC appears as the brightest block, containing ~70 % of stationary probability mass.

Figure 3. Sankey diagram of probability flow. The node sizes in this diagram show the steady-state probabilities of the three SCCs and termination state. The confirmation SCC produces the largest amount of flow towards dispatch and final states as indicated by ribbon thicknesses in the diagram.

The bar chart in Figure 4 shows both probabilistic and reward metrics. All eight metrics are normalized to their maximum values to facilitate direct comparison: completion probabilities remain at unity, error and latency expectations manifest a broader envelope, and bounded-time reachability highlights deadline performance.

Shazada Muhammad Umair Khan

PhD, Associate Professor, Department of Intelligent Systems and Cybersecurity

Khassen Akbota

Project Executor, 3rd year student of Astana IT University

Myrzabek Kamila

Project Executor, 3rd year student of Astana IT University